 |
| Alexander Graham Bell, after which the bel, and therefore the decibel, is named. |
dB
The decibel (dB) is a dimensionless unit used for quantifying the power ratio between two values. The unit is useful for describing the gain or loss in a system. It is used when characterizing amplifiers, attenuators, mixers, or RF chains as a whole. It is based on the bel and is defined as follows:A power ratio is defined as:
power ratio = ouput_power / input_power
A bel is defined as:
power in bels = log10(output_power / input_power)
A decibel is 1/10 as large as a bel so ten decibels make up one bel:
1 bel = 10 decibels
And therefore power in decibels is defined as:
power in decibels = 10 * log10(output_power / input_power)
The table below shows the loss/gain as a power ratio compared to the loss/gain in decibels for several different values:
The table below shows a amplitude ratio, power ratio (which is just the amplitude ratio squared), and associated dB value. Note that the dB range for corresponding power ratios is much smaller, i.e, -100 dB to +100 dB corresponds to 0.0000000001 to 10000000000 power range. That makes the use of dBs desirable when dealing with large power ranges. An example would be a satellite communications system where transmit antenna signal power is +14 dBW and receiver antenna signal power is -160 dBW.
dBW
dBW is an abbreviation for the power ratio in dB of the measured power referenced to one watt (1000 mW):
power in dBW = 10 * log10((output_power_watts) / 1W)
For 1mW of power, you get -30 dBW.
For 2mW of power, you get -27 dBW.
For 1W of power, you get 0 dBW.
dBm
dBm, also written as dBmW, is an abbreviation for the power ratio in decibels (dB) of the measured power referenced to one milliwatt (mW):power in dBm = 10 * log10((output power in watts)/1mW) = 10 * log10((output power in watts) / 0.001)
For 1mW power, you get 0 dBm.
For 2mW power, you get about 3 dBm.
For 1W power, you get 30 dBm.
So doubling the power is equivalent to about a 3 dBm increase.
dBm to dBW Conversion
We know the following:power in dBW = 10 * log10(output power in watts/ 1W) = 10 * log10(output power in watts)
and
power in dBm = 10 * log10(output power in watts/ 1mw) =
10 * log10(output power in watts / 0.001) =
10 * log10(output power in watts * 1/1000)
So we need to divide the dBW power ratio by 1000 to equate it to the dBm power ratio. But we know that 10 * log10(1/1000) is -30 dB.
And since we know:
log10(X * Y * Z) = log10(X) + log10(Y) + log10(Z)
we can just subtract 30 dB from the dBm value instead of dividing the power ratio by 1000 to arrive at the dBW value.
So for example, 50 dBm - 30 dB = 20 dBW.
Both dBm and dBW are used for measuring absolute power.
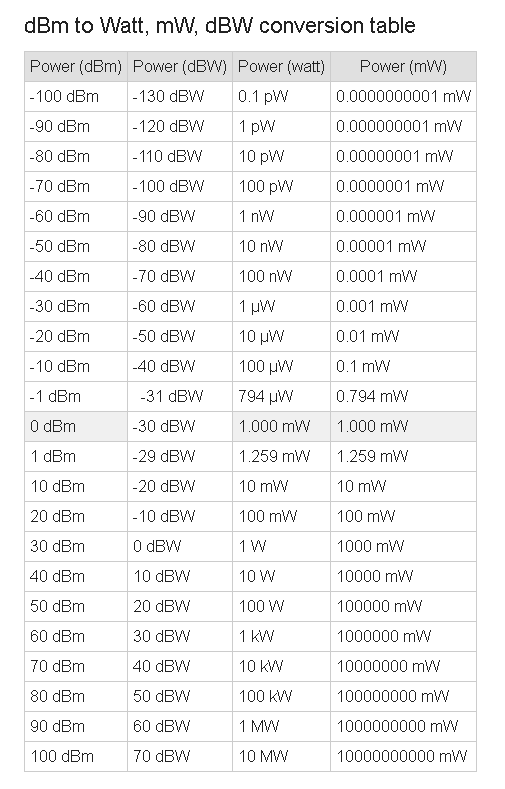
Below is a table showing the relationships between dBm, W, mW, and dBW.
References
https://en.wikipedia.org/wiki/DBmhttps://en.wikipedia.org/wiki/Decibel_watt
https://en.wikipedia.org/wiki/Decibel
http://www.allaboutcircuits.com/textbook/semiconductors/chpt-1/decibels/